Abstract
Bridge pier scouring is an important issue for safety evaluation of bridges. The existing equations for bridge pier scour prediction are mostly deterministic in nature, which do not incorporate the uncertainties in various parameters of scouring. A methodology for reliability analysis of bridge pier against scour in cohesive sediments incorporating the uncertainties of the model and input parameters are presented herein using efficient spreadsheet algorithm for first order reliability method (FORM). The influence of uncertainties, the nature of probability distribution and correlation of basic input parameters on failure probability and reliability index has been studied and described briefly herein. A sensitivity analysis was also carried out to obtain the effect of the individual random variables on the reliability of pier scour. To achieve the desired safety level in the design of pier foundation, the reliability-based safety factor is proposed.
License
This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Article Type: Research Article
AQUADEMIA, Volume 2, Issue 1, 2018, Article No: 01
https://doi.org/10.20897/awet/86715
Publication date: 10 Apr 2018
Article Views: 5392
Article Downloads: 3364
Open Access HTML Content References How to cite this articleHTML Content
INTRODUCTION
The removal of soil material surrounding a bridge foundation (piers and abutments) caused by flowing water is termed as local scour. High flow of water erodes and carries away material not only from around the piers and abutments of bridges but also from the bed and banks of streams. However, the rate of scour does not equal for all types of the bed materials but it is different for different materials. The scouring process is not only affected by nature and type of bed materials but it also depends upon type, shape, size of obstruction and on the angle of attack. The safety evaluation of bridges are very important issue. The pier foundation should be deeper than maximum possible scour depth for the safety of bridges. Hence for safe and economical design of a bridge pier foundation, a reliable assessment of possible scour depth is required.
Ettema (1980), Jain (1981), Raudkivi (1986), Melville and Sutherland (1988), Melville (1997), Coleman and Melville (2001), Muzzammil and Gnagadhariah (2003), Link (2004), Sheppard and Miller (2006) carried out comprehensive experimental investigation and they proposed model for prediction scour depth around bridge piers in noncohesive bed materials. Various form of soft computing techniques have been used to develop more refined scour prediction models at various types of hydraulics structures (Shin and Park, 2010; Balouchi et al., 2015; Ebtehaj et al., 2017; Ghazanfari-Hashemi et al., 2011; Sharafi et al., 2016; Moradi et al., 2017).
A limited study on scour around bridge piers in cohesive sediment have been reported (Briaud et al., 1999; Ting et al., 2001; Molinas and Hosny, 1999; Ansari et al., 2002; Debnath et al., 2007a; Debnath and Chaudhuri, 2010). It may probably be attributed to complex interaction of cohesive sediment transport with the vortex scour mechanism. Briaud et al. (1999) and Ting et al. (2001) conducted an experiment around a circular pier and concluded that the maximum scour depth (\(d_{s}\)) obtained from various experiments were approximately similar as that calculated by HEC-18 equation for sand (Richardson and Davis 1995). Molinas and Hosny (1999) carried out an experimental study and proposed an empirical equation for maximum scour depth (\(d_{s}\)) as function of Clay content (\(C\)) and flow Froude number (\(F_{r}\)). They reported that as increase in \(C\) results in decrease in maximum scour depth (\(d_{s}\)) whereas an increase in moisture content (\(W_{c}\)) will cause an increase in maximum scour depth. Ansari et al. (2002) conducted an experimental investigation and suggested two different scour depth prediction model for maximum scour depth (\(d_{s}\)) in different range of input parameters. They further concluded that the scouring started from sides of the pier and spread in direction of upstream for a range of \(C\) (0.05 – 0.1) and follow the same pattern for a range of \(C\) (0.2 – 0.4), whereas for \(C > 0.5\), insignificant scour occurred at the pier. Debnath and Chaudhuri (2010) carried out an experimental study for computation of scour depth in a clay-sand mixed bed around circular bridge piers. They observed that the scour depth reduced due to presence of clay in clay-sand mixture. They proposed a scour depth prediction model in dimensionless form as a function of pier Froude number, clay content, moisture content and bed shear strength. The soft computing techniques such as gene expression programming (GEP) have been applied by Danish (2014), Muzzammil et al. (2015a) and group method of data handling (GMDH) used by Muzzammil et al. (2015b) and Danish et al. (2016) for modelling of scour depth on cohesive bed for the refinement of the scour prediction model.
It is well known that the basic parameters involved in scour depth prediction models are random in nature and have uncertainties of various magnitude. The scour depth prediction model itself may also have model uncertainty. A reliability analysis is a better option to incorporate these uncertainties and provide a quantitative assessment of safety factor for pier against scouring.
The reliability analysis were applied by Johnson and Ayyub (1992), Johnson (1992), Johnson and Dock (1998), Ghosn and Johnson (2000), Yanmaz and Ustun (2001), Yanmaz (2002), Johnson and Niezgoda (2004), Siddiqui et al. (2004), Muzammil et al. (2006), Muzzammil and Siddiqui (2009), Adeel et al. (2016) and Khalid et al. (2017). The probabilistic scour depth prediction of bridge pier initially raised by Johnson and Ayyub (1992) and presented a reliable method by including uncertainties involved in various basic parameters. They used advance Monte Carlo simulation technique for computation of failure probability of bridge piers. Johnson (1996) carried out linear fuzzy regression to find out modeling uncertainty. The HEC-18 model used by Johnson and Dock (1998) for reliability analysis using the hydraulic variable of enormous storm event. A reliability-based scour depth prediction model developed by Ghosn and Johnson (2000) considering the mutual effect of earthquake and scour. Muzzammil et.al. (2006) carried out a probabilistic approach based on Coleman and Melville (2001) scour model. Khalid et al. (2017) carried out reliability analysis of Sheppard and Miller (2006) scour depth prediction model under live bed condition.
The conventional method of reliability analysis seems moderately straightforward, and evaluation of the integrals involved in this method is difficult. It is further difficult to find the nature of distribution of the random variables. It is a tough task to find the joint probability distribution of all the random variables which are responsible for scouring in the field. The approximate and simulation methods have been developed to incorporate above difficulties such as the First Order Reliability Method (FORM) and Monte Carlo Simulation Method (MCS). The FORM demonstrated by Ayyub and Haldar (1984) is easy and computationally effective technique as compare to MCS method.
The main objective of the present study is to develop a reliability-based scour depth for local scour at bridge pier in cohesive sediment. The first order reliability method (FORM) has been used for the reliability analysis. The effect of uncertainties and the probability distribution of basic input parameters on failure probability and reliability index has been studied in detail. An attempt was also made to study the influence of correlation among input parameters on reliability and the failure probability of the bridge pier. A sensitivity analysis has been carried out to study influence of random variables on the safety of pier scour. To obtain desired level of safety in the design of pier foundation, a reliability-based safety factor has been developed.
DETERMINISTIC SCOUR DEPTH PREDICTION MODEL
Hosny (1995), Gudavalli (1997), Molinas and Hosny (1999), Briaud et al. (1999), Ansari et al. (2002) and Debnath and Chaudhuri (2010) carry out a study on scour around bridge pier in cohesive bed and developed deterministic scour prediction models.
Debnath and Chaudhuri (2010) conducted an experimental study in a tilting flume of 18.3 m long, 0.9 m wide and 0.9 m deep at a constant slope of 0.001. The range of various parameters and their mean values are provided in Table 1.
|
Table 1. Range of data obtained from experimental study
|
||||||||||||||||||||||||||||||||||||||||||
The scour depth prediction model developed by Debnath and Chaudhuri (2010) from experimental study for local scour around circular pier in clay-sand mixture is reproduced here in the following form:
| \[\frac{d_{s}}{D} = 8.2F_{\text{rp}}^{0.79}C^{- 0.28}W_{c}^{0.15}\left( \frac{\tau_{s}}{\rho V^{2}} \right)^{- 0.38}\] | (1) |
where \(d_{s}\) = Maximum equilibrium scour depth; \(D\) = Pier diameter; \(F_{\text{rp}}\) = Pier Froude number; \(C\) = clay fraction by dry weight of mixture; \(W_{c}\) = moisture content by weight of dry mix; \(\tau_{s}\) = bed shear strength; \(\rho\) = mass density of water; \(V\) = depth average velocity. The dimensionless scour depth, \(d_{s}/D\), is referred herein as relative scour depth.
Laboratory scour data obtained from the Debnath and Chaudhuri (2010) has been reanalyzed here just to get more refined scour depth prediction model using Minitab software expressed as
| \[\frac{d_{s}}{D} = 4.77F_{\text{rp}}^{0.53}C^{- 0.23}W_{c}^{0.28}\left( \frac{\tau_{s}}{\rho V^{2}} \right)^{- 0.25}\] | (2) |
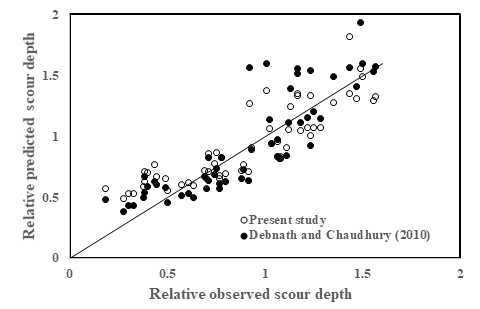
A comparative study between present and Debnath and Chaudhuri (2010) scour depth prediction models in terms of performance indices such as correlation coefficient (R), mean percentage error (MPE), mean absolute deviation (MAD) and root mean square error (RMSE) has been carried out. The expressions for R, MPE, MAD and RMSE have been provided in Appendix. The computed performance indices are shown in Table 2. This table indicates that the performance of present scour depth prediction model is slightly improved as compared with that of Debnath and Chaudhuri (2010).
|
Table 2. Comparison of performance index of between present scour depth model and Debnath and Chaudhuri (2010)
|
A scatter diagram between the relative observed and predicted scour depth has also been shown in Figure 1. This figure also indicates that the present scour prediction model is better than that of Debnath and Chaudhuri (2010).
The parameters used in Eq. 2 are random in nature and hence these parameters would have uncertainties associated with probability of occurrence. Hence to incorporate these uncertainties a probabilistic approach is required.
PROBABILISTICS SCOUR DEPTH PREDICTION MODEL
The reliability analysis of any structure is basically a probabilistic approach which predict the probability of limit state violation at any stage of a structure during its entire life. In case of bridge pier scour, if the scour depth (\(d_{s}\)) exceeds the depth of foundation (\(d_{f}\)), it is said to be limit state violation. The mathematical representation of a certain limit state of failure is known as limit state function. If limit state function gives a negative or zero value it will be in failure region and a positive value for safety. Thus, the probability of limit state of violation may be define as;
| \[P_{f} = P\left\lbrack g\left( x \right) \leq 0 \right\rbrack\] | (3) |
where \(g\left( x \right)\) is the limit state function. The limit state function in the present case may be expressed as;
| \[g\left( x \right) = d_{f} - d_{s}\] | (4) |
It is obvious from above equation that structure failure occurs if local maximum scour depth \(d_{s}\) is equal to or greater than depth of foundation \(d_{f}\). The expression for \(d_{s}\) in the limit state function is now written as,
| \(g\left( x \right) = d_{f} - 4.77\text{λF}_{\text{rp}}^{0.53}C^{- 0.23}W_{c}^{0.28}\left( \frac{\tau_{s}}{\rho V^{2}} \right)^{- 0.25}D\) | (5) |
Here \(\lambda\), \(D\), \(F_{\text{rp}}\), \(C\), \(W_{c}\), \(\tau_{s}\), \(\rho\), \(V\), and \(d_{f}\) are random variables. \(\lambda\) is a model correction factor and express as the ratio of the observed to predict scour depth (Johnson, 1992).
METHOD OF RELIABILITY ANALYSIS
The First Order Reliability Method (FORM) has been used for reliability assessment of the bridge pier against scouring. The (FORM) makes use of the first and second moments of the random variables. It is based on the first order Taylor’s series approximation of the performance function linearized at the mean values of the random variables. The FORM based on the spreadsheet-cell object-oriented constrained optimization approach developed by Low and Tang (2007) has been implemented in the present study.
Spreadsheet Algorithm for First-Order Reliability Method
Low and Tang (2007) present the excel spreadsheet platform which avoids the computations of equivalent normal means and equivalent normal standard deviations.
The matrix formulation of the reliability index \(\beta\) is
| \[\beta = \min_{x \in F}\sqrt{\left( x - \mu \right)^{T}C^{- 1}\left( x - \mu \right)}\] | (6) |
Or, equivalently
| \[\beta = \min_{x \in F}\sqrt{\left( \frac{x_{i} - \mu_{i}}{\sigma_{i}} \right)^{T}R^{- 1}\left( \frac{x_{i} - \mu_{i}}{\sigma_{i}} \right)}\] | (7) |
where \(x\) = vector representing the set of random variables\(\ x_{i}\); \(\mu\) = vector of mean values \(\mu_{i}\); \(C\) = covariance matrix; \(R\) = correlation matrix; \(\sigma_{i}\) = standard deviation; and also \(F\) denotes failure Region. Eq. 7 is preferred because correlation matrix is easier to set up.
For nonnormal variable, equivalent normal mean and equivalent normal standard deviation are calculated in such a way that the cumulative probability, as well as the probability density ordinate of the equivalent normal distribution to those of the corresponding nonnormal distribution are same.
Equivalent normal mean
| \[\mu^{N} = x - \sigma^{N}\varphi^{- 1}\left\lbrack F\left( x \right) \right\rbrack\] | (8) |
Equivalent normal standard deviation
| \[\sigma^{N} = \frac{f_{1\ \left\lbrack \varphi^{- 1}\left\lbrack F\left( x \right) \right\rbrack \right\rbrack}}{f\left( x \right)}\] | (9) |
where \(x\) is original nonnormal variate; \(\varphi^{- 1}\lbrack \bullet \rbrack\) is inverse of the cumulative probability density function of standard normal variates; \(F\left( x \right)\) is original nonnormal CDF; \(f_{1}\left\lbrack \bullet \right\rbrack\) is PDF of standard normal variates and \(f\left( x \right)\) is original nonnormal PDF.
If it is assumed that \(n_{x} = \frac{x_{i} - \mu_{i}}{\sigma_{i}}\), the Eq.7 may be reduced to
| \[\beta = \min_{x \in F}\sqrt{\left\lbrack n^{T} \right\rbrack\left\lbrack R \right\rbrack^{- 1}\left\lbrack n \right\rbrack}\] | (10) |
Eq.8 may be expressed as
|
\[\frac{x_{i} - \mu_{i}}{\sigma_{i}} = n_{i} = \varphi^{- 1}\left\lbrack F\left( x_{i} \right) \right\rbrack\] \[x_{i} = F^{- 1}\varphi\left( n_{i} \right)\] |
(11) |
Thus, each \(x_{i}\) values may be computed by varying the values \(n_{i}\) instead of varying \(x_{i}\) which is described in Low and Tang (1997; 2004). The reliability index \(\beta\) was computed directly by using Eq. 10 in excel sheets by using an array formula.
“ = sqrt (mmult (transpose (nx), mmult (minverse (crmat),nx)))” followed by “Enter” while holding down the “Ctrl” and “Shift” keys in which mmult, transpose, and minverse is Excel’s built-in functions, each being a container of program codes for matrix operations. The first and third terms under the square root sign in Eq. 10 are the equivalent standard normal vector and, being functions of \(x_{i}\). In this approach, the equivalent standard normal vector will be varied automatically during EXCEL SOLVER’s constrained optimization hence label \(n_{i}\) is used.
The objective is to find the value \(x_{i}\) such that the nonnormal cumulative probability distribution \(F(x_{i})\) at \(x_{i}\) is equal to the standard normal cumulative distribution \(\varphi(n_{i})\). The design point (\(x^{*}\)) on failure surface can be obtained by minimizing the \(\beta\) taking a constraint \(g\left( x \right) = 0\) in EXCEL SOLVER. The initial each value of \(n_{i}\) may be taken as zero.
There is no need for calculation of equivalent normal mean and equivalent normal standard deviation as in conventional method. It is therefore faster and involves less SOLVER iterations for optimization. It is also much more robust and efficient.
APPLICATION OF RELIABILITY ANALYSIS
To illustrate the present formulation, the statistics of data obtained by Debnath and chaudhuri (2010) has been used for reliability analysis and shown in Table 3. The probability distribution of the random variables have been assumed. The correlation matrix among the random variables have been shown in Table 4. The reliability analysis was carried out on Excel sheet based on spreadsheet approach developed by Low and Tang (2007). Results obtained from reliability analysis are provided in Table 5 and Table 6 in terms of reliability index (\(\beta\)) and failure probability (\(P_{f}\)).
|
Table 3. Statistics of basic variables considered in the present study
|
|
Table 4. Correlation matrix of basic variables considered in present study
|
|
Table 5. Relationship of reliability index and failure probability with safety factor for mixed distributions
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 6. Relationship of reliability index and failure probability with the safety factor for normal distributions
|
|||||||||||||||||||||||||||||||||||||||||||||||||
The safety factor (\(\text{SF}\)) has been defined herein as the ratio of the depth of foundation to the scour depth and expressed as
| \[SF = \frac{d_{f}}{d_{s}}\] | (12) |
The safety factors (\(\text{SF}\)) are generally used to incorporate design uncertainties and protect them against the failure.
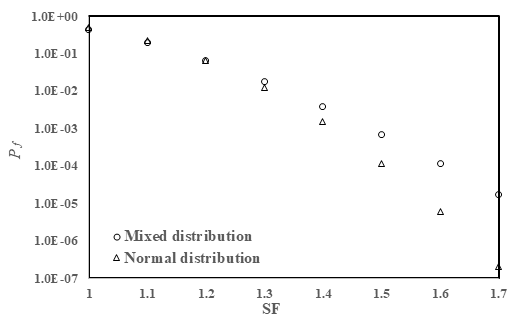
Table 5 represents the variation of reliability index and probability of failure with safety factor for uncorrelated and correlated random variables. It shows that the failure probability decreases and reliability index increases with an increase of safety factor. It may also be observed that the failure probability for correlated variables is higher than the uncorrelated variable for a particular values of safety factor.
Table 6 shows the result of reliability analysis for only normal distribution of random variables. To study the influence of probability distribution of random variable, variation of failure probability with safety factor from Table 5 and Table 6 have been shown in Figure 2. It shows that the failure probability for a safety factor 1.7 are 0.0000002 and 0.00001 for normal and mixed distribution respectively for uncorrelated variables. It may be concluded that the nature of probability distribution of random variables has a significant effect on the safety of pier in the present case.
Sensitivity Analysis
The sensitivity analysis was carried out to study the influence of various random variables on reliability of scour depth. The sensitivity factor, αi measures influence of various random variables on system safety and defined as;
| \[\alpha_{i}^{*} = - \frac{\left( \frac{\partial g}{{\partial X}_{i}} \right)^{*}}{\sqrt{\sum_{i = 1}^{n}\left( \frac{\partial g}{{\partial X}_{i}} \right)^{2*}}}\] | (13) |
The above-defined sensitivity factors have the subsequent characteristics;
1. The higher value of \(\alpha_{i}\) more is the effect of that random variable on reliability.
2. The negative value of \(\alpha_{i}\) represents resistance variables and positive value for load variables.
3. If \(\alpha_{1},\alpha_{2},\alpha_{3},\ldots,\alpha_{n}\) are the sensitivity factor for \(n\) random variable then
| \[\sum_{i = 1}^{n}\alpha_{i}^{2} = 1\ \] | (14) |
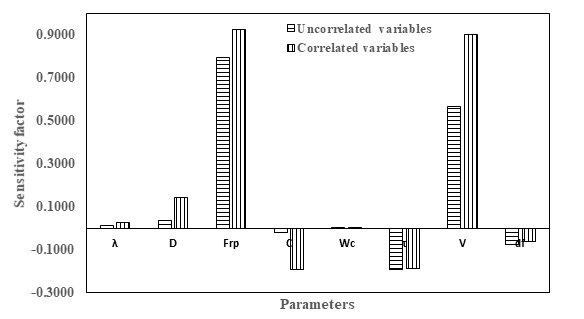
The sensitivity analysis for the various parameters are shown in Figure 3. The sensitivity factor for model correction factor, pier diameter, Froude number, velocity of flow are positive, hence, these are the load variables and it will provide favorable conditions for scour. The sensitivity factors for other parameter is negative, hence these are the resistance variable and contribute the resisting part of limit state function. The sensitivity analysis also indicate that the Froude number and velocity of flow are most significant parameters, followed by pier diameter and model correction factor. It is noted from the sensitivity analysis the correlation among the variables increase the adverse effect on reliability.
Effect of Uncertainty on Scouring Parameters
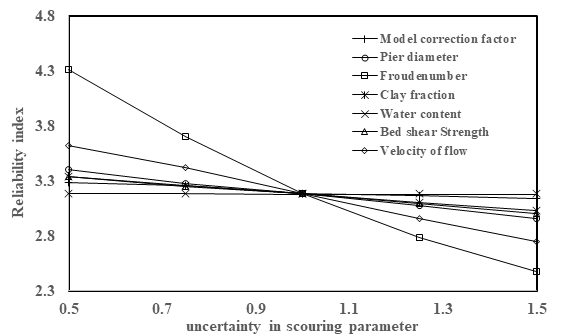
The influence of uncertainties of random variables on reliability index have been carried out. The influence on the reliability index due variation in uncertainty of scouring parameters from 0.5 to 1.5 (i.e. 50 % to 150%) has been shown in Figure 4. It may be observed that the reliability index increases with the decrease in uncertainties from 100% to 50% whereas it decreases with an increase in uncertainties from 100% to 150 % for all random variables. The reliability index decreases rapidly for Froude number and velocity of flow as compare to other parameters but the decrease in reliability index for velocity of flow is slower as compare to Froude number. The other remaining parameters have little effect on reliability index. It is already verified by sensitivity analysis, these parameters do not contribute more effect on scour.
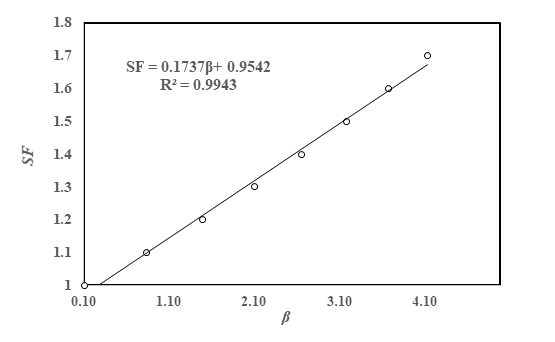
Relationship between Safety Factor and Reliability Index
The relationship between safety factor and reliability index of a bridge pier has been shown in Figure 5 for random variables. It shows that reliability index increases linearly as safety factor increases. It is clear from the figure that the distribution has insignificant effect on reliability index for lower values of safety factor but for higher values of safety factor it has significant effect.
An equation has been developed for computation of the safety factor (\(\text{SF}\)) with a coefficient of determination \(R^{2} = 0.9943\) in terms of the reliability index for mixed distribution and expressed as
| \[SF = 0.1737\beta - 0.9542\] | (15) |
The relation is not for general use, because it is based on a limited data set and assumes values of probability distribution. Other important issues such as the effects of foundation type, cost, or the consequences of failure are not adequately considered in the derivation. However, this relation may be adopted for decision for the appropriate safety factor.
CONCLUSIONS
An efficient spreadsheet based algorithm for First Order Reliability method (FORM) has been implemented in the present study for probabilistic approach of bridge pier scour prediction in cohesive sediment for uncorrelated and correlated variables. It was found that the reliability index increases with an increase in the safety factor, whereas an increase in safety factor causes the decrease in failure probability. The probability of failure is found to be higher for correlated variables as compared to that of uncorrelated variable. It was also found that the nature of probability distribution of random variables has a significant effect on the safety of pier. The clay fraction and moisture content was found to be as a resisting factor on reliability. Froude number was found to be a dominant parameter on the bridge pier failure. A relation for safety factor has been proposed in terms of reliability index for computation of reliability-based safety factor in the present analysis.
APPENDIX
| \[R = \frac{\sum_{i = 1}^{N}{\left( d_{\text{soi}} - {\overline{d}}_{\text{soi}} \right)\left( d_{\text{spi}} - {\overline{d}}_{\text{spi}} \right)}}{\sqrt{\sum_{i = 1}^{N}{\left( d_{\text{soi}} - {\overline{d}}_{\text{soi}} \right)^{2} \bullet \sum_{i = 1}^{N}\left( d_{\text{spi}} - {\overline{d}}_{\text{spi}} \right)^{2}}}}\] | (A1) |
| \[MAD = \frac{\left\lbrack \sum_{i = 1}^{N}\left| d_{\text{so}} - d_{\text{sp}} \right| \right\rbrack}{N}\] | (A2) |
| \[MPE = \frac{1}{N}\left\lbrack \sum_{i = 1}^{N}\frac{d_{\text{so}} - d_{\text{sp}}}{d_{\text{so}}} \right\rbrack \times 100\] | (A3) |
| \[RMSE = \sqrt{\frac{1}{N}\left\lbrack \sum_{i = 1}^{N}\left( d_{\text{so}} - d_{\text{sp}} \right)^{2} \right\rbrack}\] | (A4) |
References
- Adeel, A., Muzzammil, M. and Alam, J. (2016). Reliability Analysis of Pier Scour at Gravel-Bed Rivers Using FORM. International Journal of Recent Research Aspects, 3(1), 3-7.
- Ansari, S. A., Kothyari, U. C. and RangaRaju, K. G. (2002). Influence of cohesion on scour around bridge Piers. J. Hydraul. Res., 40(6), 717–729. https://doi.org/10.1080/00221680209499918
- Ayyub, B. M. and Haldar, A. (1984). Practical structural reliability techniques. J. Struct. Engng., 110(8), 1707-1724. https://doi.org/10.1061/(ASCE)0733-9445(1984)110:8(1707)
- Balouchi, B., Nikoo, M. R. and Adamowski, J. (2015). Development of expert systems for the prediction of scour depth under live-bed conditions at river confluences: Application of different types of ANNs and the M5P model tree. Applied Soft Computing, 34, 51–59. https://doi.org/10.1016/j.asoc.2015.04.040
- Briaud, J.-L, Ting, F. C. K., Chen, H. C., Gudavalli, R., Perugu, S. and Wei, G. (1999). SRICOS: Prediction of scour rate in cohesive soils at bridge piers. J. Geotech. Geoenviron. Eng., 125(4), 237–246. https://doi.org/10.1061/(ASCE)1090-0241(1999)125:4(237)
- Coleman, S. E. and Melville, B. W. (2001). Case study: New Zealand Bridge scour experiences. J. Hydraul. Eng., 127(7), 535-546. https://doi.org/10.1061/(ASCE)0733-9429(2001)127:7(535)
- Danish, M. (2014). Prediction of Scour Depth at Bridge Abutments in Cohesive Bed Using Gene Expression Programming. International Journal of Civil Engineering and technology (IJCIET), 5(11), 25-32. ISSN: 0976-6316.
- Danish, M., Alam, J. and Muzzammil, M. (2016). Scour Depth Prediction at Bridge Abutments in Cohesive Bed Using Group Method of Data Handling. Proceedings of the International Conference HYDRO-2016 held on 08-10 Dec. at CWPRS, Pune, India.
- Debnath, K., Aberle, J., Nikora, V., Westrich, B. and Muste, M. (2007a). Erosion of cohesive sediments: Re-suspension, bed load, and erosion patterns from field experiments. J. Hydraul. Eng., 133(5), 508–520. https://doi.org/10.1061/(ASCE)0733-9429(2007)133:5(508)
- Debnath, K. and Chaudhury, S. (2010). Bridge pier scour in clay-sand mixed sediments at near-threshold velocity for sand. Journal of Hydraulic Engineering, ASCE, 136(9), 597-609. https://doi.org/10.1061/(ASCE)HY.1943-7900.0000221
- Ebtehaj, I., Sattar, A. M., Bonakdari, H. and Zaji, A. H. (2017). Prediction of scour depth around bridge piers using self-adaptive extreme learning machine. Journal of Hydroinformatics, 19(2), 207–24. https://doi.org/10.2166/hydro.2016.025
- Ettema, R. (1980). Scour at bridge piers. Rep. No. 216, School of Engineering, Univ. of Auckland, New Zealand.
- Ghazanfari-Hashemi, S., Etemad-Shahidi, A., Kazeminezhad, M. H. and Mansoori, A. R. (2011). Prediction of pile group scour in waves using support vector machines and ANN. Journal of Hydroinformatics, 13(4), 609–20. https://doi.org/10.2166/hydro.2010.107
- Ghosn, M. and Johnson, P. (2000). Reliability analysis of bridge under the combined effect of scour and earthquakes. Eight ASCE Specially Conf. Probability mechanics and structural reliability (PMC2000), 164, 1-6.
- Gudavalli, R. (1997). Prediction model for scour rate around bridge piers in cohesive soils on the basis of flume tests. Ph.D. Dissertation, Texas A&M University, College Station, TX.
- Hosny, M. (1995). Experimental study of local scour around circular bridge piers in cohesive soils. Ph.D. Dissertation, Colorado State University, Fort Collins, CO.
- Jain, S. C. (1981). Maximum clear-water scour around circular piers. J. Hydraul. Div., 107(HY5), 611–626.
- Johnson. P. A. (1992). Reliability-based pier scour engineering. Journal of Hydraulic Engineering, ASCE, 118(10), 1344-1358. https://doi.org/10.1061/(ASCE)0733-9429(1992)118:10(1344)
- Johnson, P. A. and Ayyub, B. M. (1992). Assessing time variant bridge reliability due to pier scour. J. Hydraul. Engg., 118(6), 887-903. https://doi.org/10.1061/(ASCE)0733-9429(1992)118:6(887)
- Johnson, P. A. (1996). Uncertainty of hydraulic parameters. Journal of Hydraulic Engineering, ASCE, 122(2), 112-115. https://doi.org/10.1061/(ASCE)0733-9429(1996)122:2(112)
- Johnson, P. A. and Dock, D. A. (1998). Probabilistic bridge- scour estimate. Journal of Hydraulic Engineering, ASCE, 124(7), 750-754. https://doi.org/10.1061/(ASCE)0733-9429(1998)124:7(750)
- Johnson, P. A. and Niezgoda, S. L. (2004). Risk-based method for selecting bridge scour countermeasures. Journal of Hydraulic Engineering, ASCE, 130(2), 121-128. https://doi.org/10.1061/(ASCE)0733-9429(2004)130:2(121)
- Khalid, M., Muzzammil, M. and Alam, J. (2017). A Reliability-based assessment of live bed scour at bridge piers. Proceedings of International conference Hydro-2017, December 21-23, L.D. College of Engineering Ahmedabad, pp. 556-568.
- Link, O. (2004). An investigation on scouring around a single cylindrical pier in sand, Vol. 136, Mitteilungen des Institutes für Wasserbau und Wasserwirtschaft der Technischen Universität Darmstadt, Heft, Germany (in German).
- Low, B. K. and Tang, W. H. (1997a). Efficient reliability evaluation using spreadsheet. J. Eng. Mech., 123(7), 749-752. https://doi.org/10.1061/(ASCE)0733-9399(1997)123:7(749)
- Low, B. K. and Tang, W. H. (2004). Reliability analysis using object-oriented constrained optimization. Structural Safety, 26(1), 69-89. https://doi.org/10.1016/S0167-4730(03)00023-7
- Low, B. K. and Tang, W. H. (2007). Efficient Spreadsheet Algorithm for First Order Reliability Method. Journal of Engineering Mechanics, ASCE, 133(12), 1378-1387. https://doi.org/10.1061/(ASCE)0733-9399(2007)133:12(1378)
- Melville, B. W. (1997). Pier and abutment scour: Integrated approach. J. Hydraul. Eng., 125–136. https://doi.org/10.1061/(ASCE)0733-9429(1997)123:2(125)
- Melville, B. W. and Sutherland, A. J. (1988). Design method for local scour at bridge piers. J. Hydraul. Eng., 1210–1226. https://doi.org/10.1061/(ASCE)0733-9429(1988)114:10(1210)
- Molinas, A. and Hosny, M. M. (1999). Experimental study on scour around circular piers in cohesive soil. Publication No. FHWA-RD-99-186, Federal Highway Administration, U.S. Department of Transportation, McLean, VA.
- Moradi, F., Bonakdari, H., Kisi, O., Ebtehaj, I., Shiri, J. and Gharabaghi, B. (2017). Abutment scour depth modeling using neuro-fuzzy-embedded techniques. Marine Georesources & Geotechnology. https://doi.org/10.1080/1064119X.2017.1420113
- Muzzammil, M. and Gangadhariah, T. (2003). The mean characteristics of horseshoe vortex at a cylindrical pier. J. Hydraul. Res., 41(3), 285–297.
- Muzzammil, M., Siddiqui, N. A. and Siddiqui, A. F. (2006). Reliability analysis of bridge pier against local scour. Water and energy international, 63, 33-42. https://doi.org/10.1080/00221680309499973
- Muzammil, M. and Siddiqui, N. A. (2009). A reliability-based assessment of bridge pier scour in non-uniform sediments. Journal of hydraulic research, 47(3), 372-380. https://doi.org/10.1080/00221686.2009.9522008
- Muzzammil, M., Alam, J. and Danish, M. (2015a). Scour prediction at Bridge Piers in Cohesive Bed using gene expression programming. Elsevier, B.V, Aquatic Procedia, (4), 789-796. ISSN: 2214-241X.
- Muzzammil, M., Alam, J. and Danish. M (2015b). The GMDH Model for Prediction of Scour at Bridge Pier in Cohesive Bed. Proceedings of the International Conference HYDRO-2015 held on 17-19 Dec. at IIT. Roorkee India.
- Raudkivi, A. J. (1986). Functional trends of scour at bridge piers. J. Hydraul. Eng., 1–13. https://doi.org/10.1061/(ASCE)0733-9429(1986)112:1(1)
- Sharafi, H., Ebtehaj, I., Bonakdari, H. and Zaji, A. H. (2016). Design of a support vector machine with different kernel functions to predict scour depth around bridge piers. Natural Hazards, 84(3), 2145–62. https://doi.org/10.1007/s11069-016-2540-5
- Sheppard, D. M. and Miller, W., Jr. (2006). Live-bed local pier scour experiments. J. Hydraul. Eng., 635–642. https://doi.org/10.1061/(ASCE)0733-9429(2006)132:7(635)
- Shin, J. H. and Park, H. I. (2010). Neural network formula for local scour at piers using field data. Marine Georesources and Geotechnology, 28(1), 37-48. https://doi.org/10.1080/10641190903263054
- Siddiqui, N. A., Muzzammil, M. and Siddiqui, A. F. (2004). Reliability analysis of bridge pier against scouring. Second Intl. ASRANet colloquium, Network for integrating structural Safety, Risk and Reliability, Barcelona, Spain.
- Ting, F. C. K., Briaud, J.-L., Chen, H. C., Gudavalli, R., Perugu, S. and Wei, G. (2001). Flume tests for scour in clay at circular piers. J. Hydraul. Eng., 127(11), 969–978. https://doi.org/10.1061/(ASCE)0733-9429(2001)127:11(969)
- Yanmaz, A. M. and Ustun, I. (2001). Generalized reliability model for local scour around bridge piers of various shapes. Turkish J. Eng. Environ. Sci., 25, 687-698.
- Yanmaz, A. M. (2002). Dynamic reliability in bridge pier scouring. Turkish J. Eng. Environ. Sci., 26, 367-375.
How to cite this article
APA
Khalid, M., Muzzammil, M., & Alam, J. (2018). Reliability Analysis of Local Scour at Bridge Pier in Clay-Sand Mixed Sediments. Aquademia: Water, Environment and Technology, 2(1), 01. https://doi.org/10.20897/awet/86715
Vancouver
Khalid M, Muzzammil M, Alam J. Reliability Analysis of Local Scour at Bridge Pier in Clay-Sand Mixed Sediments. AQUADEMIA. 2018;2(1):01. https://doi.org/10.20897/awet/86715
AMA
Khalid M, Muzzammil M, Alam J. Reliability Analysis of Local Scour at Bridge Pier in Clay-Sand Mixed Sediments. AQUADEMIA. 2018;2(1), 01. https://doi.org/10.20897/awet/86715
Chicago
Khalid, Mohd, Mohammad Muzzammil, and Javed Alam. "Reliability Analysis of Local Scour at Bridge Pier in Clay-Sand Mixed Sediments". Aquademia: Water, Environment and Technology 2018 2 no. 1 (2018): 01. https://doi.org/10.20897/awet/86715
Harvard
Khalid, M., Muzzammil, M., and Alam, J. (2018). Reliability Analysis of Local Scour at Bridge Pier in Clay-Sand Mixed Sediments. Aquademia: Water, Environment and Technology, 2(1), 01. https://doi.org/10.20897/awet/86715
MLA
Khalid, Mohd et al. "Reliability Analysis of Local Scour at Bridge Pier in Clay-Sand Mixed Sediments". Aquademia: Water, Environment and Technology, vol. 2, no. 1, 2018, 01. https://doi.org/10.20897/awet/86715

 Full Text (PDF)
Full Text (PDF)