A New Numerical Model Coupling Modified Method of Characteristics and Galerkin Finite Element Method for Simulation of Solute Transport in Groundwater Flow System

Nilkanth Hanmantrao Kulkarni

doi:10.20897/awet/90719

INTRODUCTION

Assessment of groundwater pollution using numerical models has the challenge of getting accurate and stable numerical solutions especially in highly heterogeneous media. The proposed MMOC-GFE model in this study attempts to meet this challenge by using Eulerian-Lagrangian formulation. The newly developed model controls numerical dispersion and provides stable solutions by solving advection part and hydrodynamic dispersion part by MMOC and GFE methods respectively. It is shown that for chosen test case (Chiang et al., 1989) even with high Courant and Peclet numbers the model solutions are in close agreement with reported solutions.

An adaptive Eulerian-Lagrangian formulation (Neuman et al., 1984) solves the advective component of steep concentration front by single step reverse particle tracking of moving particles clustered around each front and the dispersive transport component is solved by Lagrangian formulation on a fixed grid. Chiang et al. (1989) discussed the model combining modified method of characteristics and mixed finite element method for solute transport simulation in groundwater flow system. The model allows arbitrary placement of injection and pumping wells within or on the boundaries of the domain together with different boundary conditions. It is found that the use of particle clusters at steep concentration fronts only caused numerical dispersion. Illangasekare et al. (1989) developed a discrete kernel approach for generating the velocity field solving the groundwater flow equation. Further the two-dimensional transient solute transport in water table aquifers is simulated by employing a method of characteristics. However, the simulation of sharp concentration fronts at injection well and divergent velocity fields at pumping well caused numerical smearing of the solutions. Garder et al. (1964) proposed a method of characteristic technique is for the solution of the solute transport equation which uses imaginary moving particles to represent solute mass and to calculate the concentration change at a given point in the domain for each time step. Goode (1990) modified the conventional USGS MOC, 1988 model by using bilinear interpolation schemes for velocity interpolation. But the heterogeneities at the cell interfaces require the use of higher order interpolation schemes to accurately simulate advective transport by method of characteristics. Zhang et al. (1993) proposed a computationally efficient Eulerian-Lagrangian method for solving advection-dispersion equation in both steady and transient velocity field. The method uses single step reverse particle tracking technique for steep concentration fronts and separate weighting factors which relate to grid Peclet and Courant numbers are used for upstream and downstream region of the advection front. In transient velocity field the model determines the weighting factors automatically based on the mass balance errors. This model is found to be more suitable for the solution of the advection dominated problems. Frolkovic (2002) discussed a flux based method of characteristics for simulation of contaminant transport in flowing groundwater. This method combines advantages of numerical discretizations by finite volume methods and by methods of characteristics. This method is further extended for complex transport problems on multidimensional unstructured computational grids. It is reported that this method is difficult to implement for general computational grids and also it suffers from choice of time steps. (Lichtner, 2002) applied the new form of the dispersion tensor involving axisymmetric media utilizing particle tracking techniques. It is demonstrated that for the case of spatially variable flow the drift term of dispersion must generally be included in the particle tracking algorithm to obtain accurate results. Banas (2004) solved non-linear convection-diffusion equation using method of characteristics. The features of the scheme are demonstrated for one-dimensional numerical experiment. Pinder and Gray (1977) discussed Galerkin finite element formulation to solve dispersion part of the solute transport equation. Kinzelbach and Frind (1986) used two-dimensional Galerkin finite element model with linear elements for solution of dispersion equation and effect of design of grid orientation on model accuracy is also investigated. Sheu and Chen (2002) solved the unsteady advection–diffusion equation using finite element model which employs a quadratic basis function to approximate the contaminant concentration. The development of a weighted residuals finite element model involves constructing a biased test function to retain the scheme stability for wide ranges of values of the physical coefficients. Igboekwe (2014) examined the movement of water solute from the surface of the earth to the aquifer and also to assess the impact of existing or proposed activity on the quality and quantity of groundwater through the use of groundwater flow and solute transport models. Finite element method is used for finding approximate solutions of partial differential equations as well as that of integral equations. The solution approach is based on either eliminating the differential equation completely or rendering the partial differential equation into an approximating system of ordinary differential equation. It is found that the order of the interpolation function has greater effect on solute transport solutions than groundwater flow solutions.

The objectives of this study are i) to develop and verify a computationally efficient numerical model coupling modified method of characteristics and Galerkin finite element method for solving advection and dispersion parts of the solute transport equation, respectively, ii) to verify the accuracy and stability of model results by comparing with reported solutions and iii) to analyze the effects of porosity, dispersivity and pumping rate on solute concentration distribution.

MATHEMATICAL FORMULATION

Groundwater Flow Equation

The governing equation of two-dimensional and transient groundwater flow in heterogeneous unconfined aquifer with pumping and injection wells is given as (Illangasekare et al., 1989).

\[S_{y}\frac{\partial\ h}{\partial\ t}\ = \frac{\partial^{2}\ (K_{\text{xx}}h^{2})}{\partial\ x^{2}}\ + \frac{\partial\ ^{2}(K_{\text{yy}}h^{2})}{\partial\ y^{2}} \pm \ \sum_{i\ = 1}^{n}{Q_{i}\ \delta\ (x_{o} - x_{i},\ y_{o} - y_{i}))\ }\]

(1)

where \(S_{y}\) is the specific yield in percent, \(h\) is hydraulic head [\(L\)], \(t\) is the time [\(T\)], \(k_{\text{xx}}\)and \(k_{\text{yy}}\) are hydraulic conductivities [\(L\ T^{- 1}\)],\(\ Q\)is pumping/injection rates (+ for pumping and - for injection) [\(L^{3}\ T^{- 1}\)],\(n\) total number of pumping/injection wells, \(x_{o}\),\(y_{o}\)are Cartesian coordinates of the origin [\(L\)], \(x_{i}\),\(y_{i}\)are the Cartesian coordinates of the location of pumping/injection well [\(L\)].

Equation (1) is subject to the following initial condition which is given as

\[\begin{matrix} h(x,y,0) = h_{0} & , & (x,y) \in \Omega \\ \end{matrix}\]

(2)

where \(h_{0}\) is the initial head [\(L\)] over the aquifer domain \(\Omega\) [\(L^{2}\)].

Equation (1) is subject to the following Dirichlet and Neumann boundary conditions

\[\begin{matrix} h(x,y,t) = h_{1} & , & (x,y) \in \Gamma_{1};\ t \geq 0 \\ \lbrack\{ q_{b}(x,y,t)\} - \lbrack\text{k h}\rbrack\nabla h(x,y,t)\rbrack^{'}\{ n\} = 0 & , & (x,y) \in \Gamma_{2};\ t \geq 0 \\ \end{matrix}\]

(3)

where \(h_{1}\) is the specified head over aquifer boundary \(\Gamma_{1}\), [\(L\)],\(q_{b}\)is the specified flux across boundary \(\Gamma_{2}\) [\(L\ T^{- 1}\)], [\(\lbrack k\ h\rbrack\ \nabla h(x,y,t)\)] is the groundwater flux due to head gradient [\(L\ T^{- 1}\)] and \(n\)is the normal unit vector in outward direction.

The x- and y- components of groundwater flow velocity are given as:

\[v_{x}\ = \ - \ \frac{\partial}{\partial\ x}(\frac{k_{\text{xx}} \times \ h}{\theta})\]

\[v_{y}\ = \ - \ \frac{\partial}{\partial\ x}(\frac{k_{\text{yy}} \times \ h}{\theta})\]

(4)

where \(\theta\) is the effective porosity of the aquifer and \(v_{x}\), \(v_{y}\) are velocity components [\(L\ T^{- 1}\)].

Solute Transport Equation

The governing equation of solute transport in two-dimensional transient groundwater flow system with pumping/injection wells can be given as (Illangasekare et al., 1989),

\[R\frac{\partial\ c}{\partial\ t}\ = \frac{\partial^{2}\ (D_{\text{xx}}\ c)}{\partial\ x^{2}}\ + \frac{\partial^{2}\ (D_{\text{yy}}\ c)}{\partial\ y^{2}} - V_{x}\frac{\partial\ c}{\partial\ x} - V_{y}\frac{\partial\ c}{\partial\ y} \pm \ \sum_{i\ = 1}^{n}{Q_{i}\frac{(c - c_{i})}{\text{θ }h}\ \delta\ (x_{o} - x_{i},\ y_{o} - y_{i})}\]

(5)

where \(R\) is the retardation factor [dimensionless], \(c\)is the ambient solute concentration [\(\text{ppm}\)], \(D_{\text{xx}}\), \(D_{\text{yy}}\) are hydrodynamic dispersion coefficients [L²T^-1], \({c_{i}}^{'}\)is solute concentration of the pumped/injected water at \(i\)th well point [\(\text{ppm}\)], \(\text{n}\ \)is the number of pumping/ injection well points in the domain.

An initial concentration of the solute is prescribed in the entire aquifer domain \(\Omega\) by

\[\begin{matrix} c(x,\ y,\ 0) = c_{0}\left( x,y \right) & , & (x,y) \in \Omega \\ \end{matrix}\]

(6)

where \(c_{0}\) is the initial solute concentration [ppm].

Equation (1) is subject to the following Dirichlet boundary condition and Neumann boundary conditions which are given as

\[\begin{matrix} c\left( x,y,t \right) = c_{1} & , & \left( x,y \right) \in \Gamma_{1};\ t \geq 0 \\ \left\lbrack \left\{ \text{vc}\left( x,y,t \right) \right\} - \left\lbrack D \right\rbrack\nabla c\left( \ x,y,t \right) \right\rbrack^{'}.\left\{ n \right\} = vc^{'} & , & (x,y) \in \Gamma_{2}\ ;\ t \geq 0 \\ \end{matrix}\]

(7)

where \(c_{1}\) is the prescribed solute concentration over aquifer domain boundary\(\Gamma_{1}\), [ppm], where \(vc^{'}\)is the specified advective solute flux across the boundary \(\Gamma_{2}\)[M/L³/T] and \(\lbrack D\rbrack\ \nabla\ c\)is the dispersive solute flux across the boundary\(\ \Gamma_{2}\) [M/L³/T].

The hydrodynamic dispersion coefficients in the tensor form can be given as (Zhang et al., 1993).

\[\begin{bmatrix} D_{\text{xx}} & D_{\text{xy}} \\ D_{\text{yx}} & D_{\text{yy}} \\ \end{bmatrix}\ = \ \frac{\alpha_{L}}{\left| \overline{v} \right|}\ \left| \begin{matrix} v_{x}^{2} & v_{x}v_{y} \\ v_{x}v_{y} & v_{y}^{2} \\ \end{matrix} \right|\ + \frac{\alpha_{T}}{\left| \overline{v} \right|}\ \left| \begin{matrix} v_{y}^{2} & - v_{x}v_{y} \\ - v_{x}v_{y} & v_{x}^{2} \\ \end{matrix} \right|\]

(8)

where\(\ \alpha_{L}\) and \(\alpha_{T}\) are longitudinal and transverse dispersivities, respectively [\(L\)] and \(\left| \overline{v} \right|\) is the magnitude of the groundwater flow velocity [\(LT^{- 1}\)].

NUMERICAL METHODS

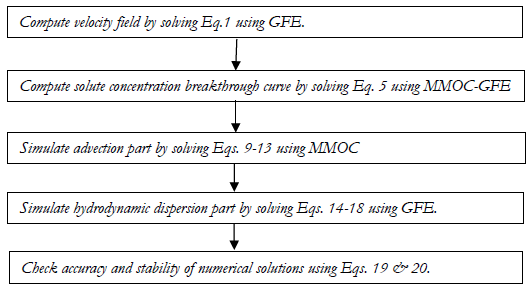
The flow chart in Figure 1 describes the various steps involved in MMOC-GFE Model.

Figure 1. Flow Chart of MMOC-GFE Model

Modified Method of Characteristics

The modified method of characteristics (MMOC) is proposed as a variant of the conventional USGS-MOC model (Konikow et al., 1978). Unlike the conventional USGS-MOC model, the MMOC method solves the advection part of solute transport equation using real fluid particles. Following steps are involved in MMOC model:

Step 1. At the start of the simulation, a set of fluid particles are generated in the block centered finite difference grid. Each fluid particle has assigned the solute concentration equal to the concentration of the respective grid to which it belongs.

Step 2. The Equation 5 is rearranged in the following form using material derivative term as,

\[\frac{\text{Dc}}{\text{Dt}} \cong \left( R\frac{\partial c}{\partial t} + v_{x}\frac{\partial c}{\partial x} + v_{y}\frac{\partial c}{\partial y} \right) = D_{\text{xx}}\frac{\partial^{2}c}{\partial x^{2}} + D_{\text{yy}}\frac{\partial^{2}c}{\partial y^{2}} \pm \sum_{i = 1}^{n}{\frac{(c - {c_{i}}^{'})}{\theta h}Q_{i}}\delta(x_{o} - x_{i},y_{o} - y_{i})\]

(9)

Step 3. The left hand side term of the above equation is solved using modified method of characteristics which involves the tracking of particles backward in time along characteristic lines. Thus the particle location at the base of the characteristic curve represents the location of the drifting particle at the previous time level, the slope of characteristic curves representing velocity components are used to compute the advective transport as follows:

\(\frac{d\ x}{d\ t} = \ v_{x}\), \(\frac{d\ y}{d\ t} = \ v_{y}\)	(10)
\[\delta x_{i,j}^{t} = v_{x_{i,j}} \times \Delta t,\ \delta y_{i,j}^{t} = v_{y_{i,j}} \times \Delta t\]	(11)

where \(\delta x_{i,j}^{t}\) and \(\delta y_{i,j}^{t}\ \)are the advective displacements in x-and y-directions, respectively [L].

Step 4. After each time step, the concentration in the grid is updated by computing the concentration change due to advection alone as follows:

\[\frac{d\ c}{d\ t} = \ \frac{\partial\ c}{\partial\ t} + \frac{d\ x}{d\ t}\frac{\partial\ c}{\partial x} + \frac{d\ y}{d\ t}\frac{\partial\ c}{\partial y}\]

(12)

Step 5: Using bilinear interpolation scheme (Goode, 1990), from the quadrantal location of particles, the concentration at the grid point is updated as follows:

\[{c^{a}}_{i,j}^{\ t\ + \Delta t} = {c_{R}^{a}}^{t} = (1 - f_{y})\ \left\{ (1 - \text{fx})\ (c_{i,j}^{t}) + (f_{x})\ (c_{i - 1,j}^{t}) \right\}\ + \ (f_{y})\left\{ (1 - \text{fx})\ (c_{i,j - 1}^{t}) + (f_{x})\ (c_{i - 1,j - 1}^{t}) \right\}\]

(13)

where \({c^{a}}_{i,j}^{t + \Delta t}\)is the concentration at the grid point after advective transport, [\(\text{ppm}\)]; \(R\)is the location of the base of the characteristic curve; \(f_{x} = \ \frac{(\Delta x - \delta x_{i,j}^{t})}{\text{Δ }x}\)and\(f_{y} = \ \frac{(\Delta y - \delta y_{i,j}^{t})}{\text{Δ }y}\)are factors of bilinear interpolation; (\(i - 1,j\ ;\ \ i - 1,\ j - 1;\ \ i,j - 1\ ;\ \ i,j\)) are the indices of the closest grid point for given location of the particle.

Galerkin Finite Element Method

The Galerkin finite element method (GFE) is used to compute the change in nodal concentration due to hydrodynamic dispersion as follows:

Step 1: The second-order hydrodynamic dispersion term in Equation (5) is approximated using GFE method. It uses Green function to yield the following system of algebraic linear equations (Pinder and Gray, 1977),

\[\left( \left\lbrack A \right\rbrack + \frac{1}{\text{Δ }t}\ \left\lbrack B \right\rbrack \right)\ \left\{ c_{L}^{t + \Delta t} \right\}\ = \ \left( \frac{1}{\text{Δ }t}\ \left\lbrack B \right\rbrack \right)\ \left\{ c_{L}^{t} \right\}\ + \left\{ d_{L} \right\} + \left\{ g_{L} \right\}\]

(14)

where \(\left\lbrack A \right\rbrack\) is the global conductance matrix which is formed by assembling the elemental conductance matrices \(\left\lbrack A_{L}^{e} \right\rbrack\) which is given as,

\[A_{L}^{e} = \iint_{e}^{}\left( D_{\text{xx}}\frac{\partial\overset{\land}{c_{L}^{e}}}{\partial x}\frac{\partial N_{L}^{e}}{\partial x} + D_{\text{yy}}\frac{\partial\overset{\land}{c_{L}^{e}}}{\partial y}\frac{\partial N_{L}^{e}}{\partial y} \right)\text{dxdy} = \frac{D_{\text{xx}}}{4\ A^{e}}\begin{bmatrix} b_{i}^{e}\ b_{i}^{e} & b_{i}^{e}\ b_{j}^{e} & b_{i}^{e}\ b_{k}^{e} \\ b_{j}^{e\ }b_{i}^{e} & b_{j}^{e}\ b_{j}^{e} & b_{j}^{e}\ b_{k}^{e} \\ b_{k\ }^{e}b_{i}^{e} & b_{k}^{e}\ b_{j}^{e} & b_{k}^{e}\ b_{k}^{e} \\ \end{bmatrix} + \frac{D_{\text{yy}}}{4A^{e}}\begin{bmatrix} c_{i}^{e}\ c_{i}^{e} & c_{i}^{e}\ c_{j}^{e} & c_{i}^{e}\ c_{k}^{e} \\ c_{j}^{e}\ c_{i}^{e} & c_{j}^{e}\ c_{j}^{e} & c_{j}^{e}\ c_{k}^{e} \\ c_{k}^{e}\ c_{i}^{e} & c_{k}^{e}\ c_{j}^{e} & c_{k}^{e}\ c_{k}^{e} \\ \end{bmatrix}_{\ }\]

(15)

\(\left\lbrack B \right\rbrack\) is the global storage matrix which is assembled from elemental storage matrices \(\left\lbrack B_{L}^{e} \right\rbrack\) which is given as,

\[\begin{matrix} B_{L}^{e} = \iint_{e}^{}{R^{e}\frac{\partial\overset{\land}{c_{L}^{e}}}{\partial t}N_{L}^{e}}\text{dx dy} = \iint_{e}^{}{R^{e}N_{L}^{e}N_{L}^{e}}\text{dx}\ \text{dy} = R^{e}\frac{A^{e}}{12}\begin{bmatrix} 2 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 2 \\ \end{bmatrix} & , & L = i \neq j \neq k \\ \end{matrix}\]

(16)

\(\left\{ d_{L} \right\}\) is the global load vector which is assembled from elemental load vectors \(\left\{ d_{L}^{e} \right\}\) which is given as,

\[\begin{matrix} d_{L}^{e} = \iint_{e}^{}{\left( \sum_{i = 1}^{n_{w}}(\overset{\land}{c_{L}^{e}} - {c_{i}^{'}}^{\ })Q_{i}^{e}\text{ δ }\left( x_{o} - x_{i}^{e},\ y_{o} - y_{i}^{e} \right) + \sum_{j = 1}^{n_{p}}{(\overset{\land}{c_{L}^{e} - c_{i}^{'}})q_{j}^{e} +}\left( \frac{\overset{\land}{c_{L}^{e}}{S_{y}}_{L}^{e}}{T_{\ }^{e}}\frac{\partial\ \overset{\land}{h_{L}^{e}}}{\partial\ t} \right) \right)N_{L}^{e}\ \text{dx}\ \text{dy}} = \\ \ \left( (\overset{\land}{c_{L}^{e}} - {c_{i}^{'}}^{\ })Q_{i}^{e}\text{ δ }\left( x_{o} - x_{i}^{e},\ y_{o} - y_{i}^{e} \right)\frac{1}{3} + \sum_{j = 1}^{n_{p}}{(\overset{\land}{c_{L}^{e} - c_{i}^{'}})q_{j}^{e}\frac{A^{e}}{3} +}\left( \frac{\overset{\land}{c_{L}^{e}}{S_{y}}_{L}^{e}\ }{T_{L}^{e}}\frac{\left( h_{L}^{t + \Delta t} - h_{L}^{t} \right)}{\text{Δ }t} \right)\frac{A^{e}}{3} \right) \begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix} \\ \end{matrix}\]

(17)

\(\left\{ g \right\}\ \)is the global boundary flux vector which is assembled from the elemental boundary flux vectors \(\left\{ g_{L}^{e} \right\}\) which is given as,

\[g_{L}^{e} = \int_{\Gamma^{e}}^{}{\ \left( D_{\text{xx}}^{e}\frac{\partial\ \overset{\land}{c_{L}^{e}}}{\partial x}\ n_{x} + D_{\text{yy}}^{e}\frac{\partial\ \overset{\land}{c_{L}^{e}}}{\partial y}\ n_{y} \right)}\ N_{L}^{e}\ d\sigma = \left( c_{L}^{e} \frac{{q_{\text{bx}}}_{L}^{e}}{D_{\text{xx}}^{e}}\ \left( \frac{d\text{σ}\ _{y}^{e}}{2} \right)\ + c_{L}^{e} \frac{{q_{\text{by}}}_{L}^{e}}{D_{\text{yy}}^{e}}\ \left( \frac{d\text{σ}_{x}^{e}}{2} \right) \right) \begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix}\]

(18)

Step 2: From the concentration distribution obtained using Equation (13) the change in concentration due to hydrodynamic dispersion distribution i.e. \({c^{d}}_{i,j}^{t + \Delta t}\) is obtained by Equation (14).

Step 3: After every time step, the final concentration at a node is computed by adding the change in concentration due to advection and dispersion.

Numerical Stability and Accuracy

The stability of the transport model solutions is checked by the criteria of Courant and Peclet numbers which are given as (Daus et al., 1986),

\[C_{x}\ = \ \frac{v_{x}\ \times \ \Delta\ t}{T_{\text{xx}}}\ \leq \ 1\ ,\ C_{y}\ = \ \frac{v_{y}\ \times \ \Delta\ t}{T_{\text{yy}}}\ \leq \ 1;\ P_{x}\ = \ \frac{v_{x}\ \times \ \Delta\ x}{D_{\text{xx}}}\ \leq \ 2\ ,\ P_{y}\ = \ \frac{v_{y}\ \times \ \Delta\ y}{D_{\text{yy}}}\ \leq \ 2\ \]

(19)

where \(C_{x}\), \(C_{y}\)and \(P_{x}\),\(\ P_{y}\)are Courant and Peclet numbers, respectively.

The accuracy of the transport model solutions is verified by the criteria of mass balance error which is given as,

\[E_{c}\ = \ \frac{100\ \left( \text{Δ}Mf_{c}^{T} - \Delta\ Ms_{c}^{T} \right)}{M_{c}^{0}}\]

(20)

where \(E_{c}\) is the average mass balance error [percent], \(\text{Δ}Mf_{c}^{T}\)is the net solute flux [ppm], \(\text{Δ}Ms_{c}^{T}\)is the change in solute mass stored [ppm] and \(M_{c}^{0}\)is the initial solute mass [ppm].

Test Case

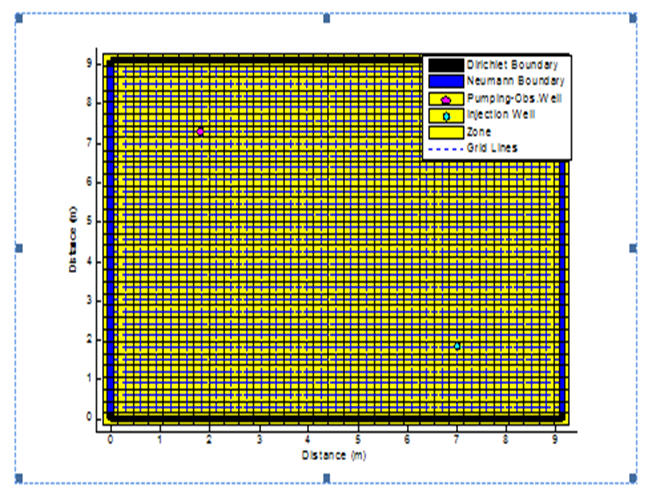
For the test case an example problem (Chiang et al., 1989) is chosen as shown in Figure 2. The purpose of this test case to study the effect of porosity, dispersivity and pumping rate on solute concentration distribution. Test case involves a two-dimensional square aquifer of size 9.14 m as shown in Figure 1. Aquifer domain is discretized into square 30 \(\times\) 30 grids and 1800 triangular elements each of size 0.31 m. A pumping well situated at location (1.8 m, 1.8 m) extracts the contaminated water at the constant discharge rate of 0.279 m³/d. This well also acts an observation well. The point source of contamination is the injection well situated at location (7.2 m, 7.2 m) constantly injects the contaminant in the aquifer with constant injection rate of 0.279 m³/d. The solute mass introduced to aquifer at injection well is removed by pumping well thereby remediating the aquifer. The flow parameters used are: hydraulic conductivity;\(k\)=0.41 m/d, specific yield;\(S_{y}\)=0.1,effective porosity;\(\theta\)=0.1.The transport parameters are: longitudinal dispersivity;\(\alpha_{L}\)=0.914 m and transverse dispersivity;\(\text{\ α}_{T}\)=0.00914 m. The time parameters are: time step size; \(\Delta t\)=0.1 day, total simulation time; \(T\)= 20 days.

Figure 2. Schematic of the Test Case used for the simulation of solute transport in two-dimensional transient groundwater flow under the combined pumping and injection well condition

RESULTS AND DISCUSSION

Velocity Field

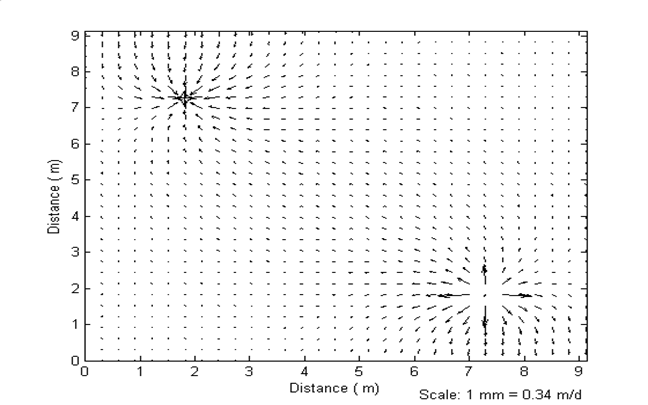
Figure 3 shows the velocity field of the test case described above by solving Equation (1) using Galerkin finite element method. The velocity field is obtained for chosen hydraulic conductivity filed. From Figure 3 the stream lines show that the convergent and divergent flow field is developed at the location of injection and pumping wells respectively. It is found that at the source and sink point for same pumping and injectin rates the resultant velocity is observed to be 1.7 m/d.

Figure 3. Velocity field

Verification of MMOC=GFE Model

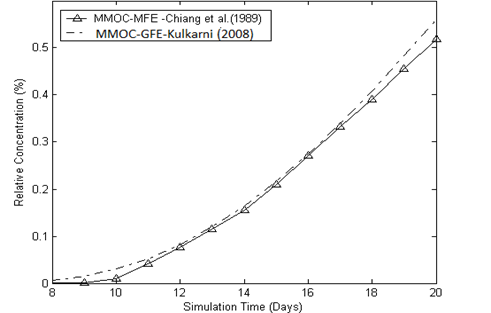
Figure 4 shows the comparison of solute concentration breakthrough curves obtained by the MMOC-GFE model with the reported solution (Chiang et al., 1989). It is found that both the breakthrough curves match very closely during the simulation period from 12 to 17 days. However they deviate in initial and final stages of simulation up to 10% due to numerical dispersion. The 56% injected solute reaches at observation point after 20 days.

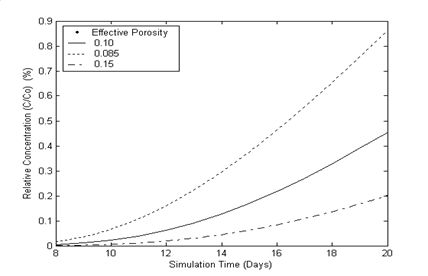
Figure 4. Comparison of the MMOC-GFE model solutions with reported solutions

Effect of Porosity

Figure 5 shows the effect of porosity on solute concentration distribution. Three different values of porosity as base value i.e. 0.10 and 15% less and 15% high are considered. It is observed from the Figure 5 that the breakthrough curve simulated with the porosity of 0.15 deviates at the end of 20 days period by an order of 65% .It is also shown that for higher values of porosity which is resulting into higher volumes of groundwater flow in the given aquifer volume thus lowering the solute mass concentration. Thus the physical effect of porosity variation is properly simulated by proposed model comparison of three concentration breakthrough curves simulated by FEFLOW-MMOCSOLUTE model with three different values of the effective porosity.

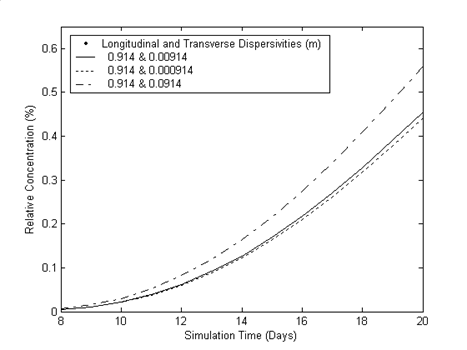
Figure 5. Effect of porosity on solute concentration distribution

Effect of Transverse Dispersivity

Figure 6 shows the comparison of the concentration breakthrough curves simulated with the three values of the transverse dispersivity. The magnitude of transverse dipersivity is varied as one order less and one order higher respectively compared to its base value (0.00914) i.e. 0.0914 and 0.000914 m, respectively. It is found that the concentration breakthrough simulated with the dispersivity of 0.0914 deviates from the breakthrough curve simulated with the initially chosen dispersivity value by 7%. The concentration breakthrough simulated with the dispersivity of 0.000914 m deviates from the breakthrough curve simulated with the initially chosen value of the dispersivity by 22%.

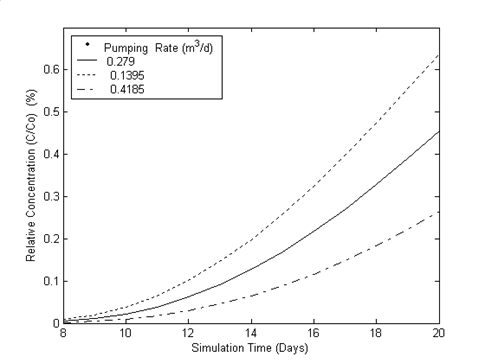
Figure 6. Effect of transverse dispersivity on solute concentration distribution

Effect of Pumping Rate

Figure 7 shows the comparison of the three concentration breakthrough curves at the pumping well which is considered as observation well. The initial pumping rate of 0.279 m³/d varied to its half (0.1395 m³/d) and double value of 0.418 m³/d. Due to high pumping rate the concentration goes down and due to low pumping rate the less concentration mass is taken out from the contaminated aquifer resulting into the occurrence of higher concentrations at the observation well. This physical condition is adequately simulated by numerical models. The concentration breakthrough simulated with increased pumping rate drops down to 46% of that of the concentration for the given pumping rate and for decreased pumping rate the breakthrough concentration rises to 35% of that of the concentration for the given pumping rate.

Figure 7. Effect of pumping rate on solute concentration distribution

CONCLUSIONS

Verification of the MMOC-GFE model for chosen test case show that the model results are in close agreement with reported solutions.
Investigations pertaining to effect of space and time discretizations on proposed model reveal that the model produce stable and accurate results for high values of Courant and Peclet numbers.
It is found that the solute concentration arrival time at observation point increases by 22% for one order less value of transverse dispersivity from its base value because of slow dispersive movement of solute.
It is noticed from model solutions that the higher values of effective porosity results into increased volume of groundwater flow thereby lowering solute mass concentration.
Model results show accurate simulation of physical condition that the higher pumping rate lowers the solute concentration at the observation well.

Banas, L. (2004). Solution of convection-diffusion equation by the method of characteristics. Journal of Computational and Applied Mathematics, 168, 31-39. https://doi.org/10.1016/j.cam.2003.12.003
Chiang, C. Y., Wheeler, M. F. and Bedient, P. B. (1989). A modified method of characteristics technique and mixed finite elements method for simulation of groundwater solute transport. Water Resources Research, 25(7), 1541-1549. https://doi.org/10.1029/WR025i007p01541
Frolkovic, P. (2002). Flux-based method of characteristics for contaminant transport in flowing groundwater. Computing and Visualization in Science, 5, 73-83. https://doi.org/10.1007/s00791-002-0089-1
Garder, A. O., Peaceman, D. W. and Pozzi, A. L. Jr. (1964). Numerical calculation of multidimensional miscible displacement by the method of characteristics. Society of Petroleum Engineers Journal, 4(1), 26-36. https://doi.org/10.2118/683-PA
Goode, D. J. (1990). Particle velocity interpolation in block-centered finite difference groundwater flow models. Water Resources Research, 26(5), 925-940. https://doi.org/10.1029/WR026i005p00925
Igboekwe, M. U. (2014). Finite Element Method of Modeling Solute Transport in Groundwater Flow. The Pacific Journal of Science and Technology, 15(1), 85-92. https://doi.org/10.1029/WR025i005p00857
Illangasekare, T. H. and Doll, P. (1989). A discrete kernel method of characteristics model of solute transport in water table aquifers. Water Resources Research, 25(5), 857-867.
Kulkarni. (2008). Numerical Experiments on the Solute Transport in Groundwater Flow Systems, Ph.D. Thesis, IIT Bombay, India.
Kinzelbach, W. K. H. and Frind, E. O. (1986). Accuracy criteria for advection-dispersion models. VI International Conference on Finite Elements in Water Resources, Lisbon, Portugal.
Konikow, L. F. and Bredehoeft, J. D. (1978). Computer model of two-dimensional solute transport and dispersion in groundwater. Techniques of Water Resources Investigations, USGS Book 7, U.S. Government Printing Office, Washington D. C.
Lichtner, P. C., Kelkar, S. and Robinson, B. (2002). New form of dispersion tensor for axisymmetric porous media with implementation in particle tracking. Water Resources Research, 38(8), 1-16. https://doi.org/10.1029/2000WR000100
Neuman, S. P. (1984). Adaptive Eulerian-Lagrangian finite element method for advection-dispersion. International Journal of Numerical Methods in Engineering, 20, 321-337. https://doi.org/10.1002/nme.1620200211
Pinder, G. F. and Gray, W. G. (1977). Finite Element Simulation in Surface and subsurface Hydrology, Academic Press, San Diego.
Sheu, T. W. H. and Chen, Y. H. (2002). Finite element analysis of contaminant transport in groundwater. Applied Mathematics and Computation, 127, 23-43. https://doi.org/10.1016/S0096-3003(00)00160-0
Zhang, R., Huang, K. and van Glenuchten, M. T. (1993). An efficient Eulerian- Lagrangian method for solving solute transport problems in steady and transient flow fields. Water Resources Research, 29(12), 4131-4138. https://doi.org/10.1029/93WR01674

Aquademia

Abstract

Keywords

License